Prof. Ing. Maurizio Froli¹, Dr. Ing. Gerardo Masiello², Dr. Ing. Francesco Gianola³.
¹ Dipartimento di Ingegneria Strutturale, Università di Pisa
² Libero professionista in Pisa
³ Von Karman Institute, Belgium
ABSTRACT:L’analisi del comportamento statico e dinamico di una struttura mediante modellazioni agli elementi finiti è fortemente influenzata dalle ipotesi di base sulle condizioni di vincolo, le proprietà meccaniche dei materiali ecc.. Non sempre è possibile verificare a priori la validità delle ipotesi assunte alla base del calcolo con i reali parametri che caratterizzano il comportamento statico e dinamico della struttura. Se però si dispone di informazioni sul reale comportamento della struttura allora il modello teorico può essere corretto e tarato con tecniche di Model Updating (Ewins, 2000). In questa nota viene presentato un esempio di identificazione dinamica nel dominio delle frequenze applicata alla copertura metallica di fine ottocento del salone centrale del Mercato coperto delle Vettovaglie di Livorno, costituita principalmente da capriate trasversali con schema statico di arco a tre cerniere e catena, poste ad un interasse costante di 5 metri.
La struttura è stata sottoposta a cicli di prove di carico statiche e dinamiche con forzante di tipo impulsivo indotta da una massa battente in caduta libera da diverse altezze. Attraverso le prove statiche sono state ricavate direttamente informazioni sul comportamento deformativi della struttura attraverso le quali è stata eseguita una prima correzione del modello FEM.
Successivamente il processo di identificazione dinamica è stato condotto con il Peak Picking Method (Ewins, 2000), caratterizzato dalla estrazione dei picchi che individuano le frequenze naturali dei modi propri di vibrare della struttura mediante diretta osservazione degli spettri in frequenza ricavati sperimentalmente.
Seguiranno ulteriori elaborazioni dei dati sperimentali eseguite con il metodo MDOF Circle Fit Method (Ewins, 2000), attraverso una preliminare valutazione della funzione complessa inertanza (FRF) che nella rappresentazione in un piano di Nyquist descrive un cerchio nell’intorno di una frequenza naturale del sistema.
Figura 1. Sezione trasversale del Mercato Centrale di Livorno (Ricordi di Architettura, serie II, vol. VI)
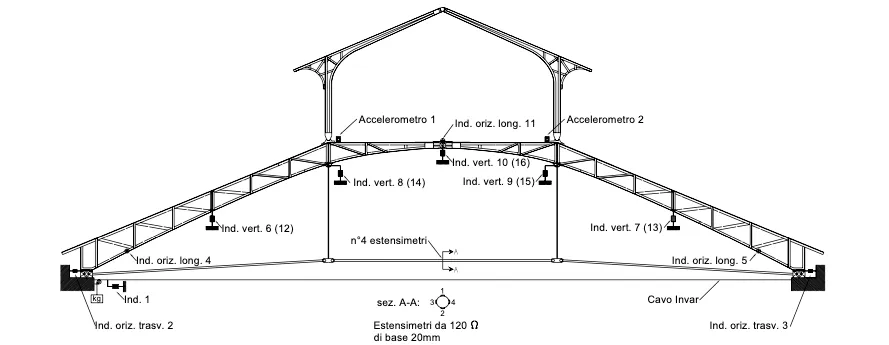
Figura 2. Dislocazione e numerazione della strumentazione di misura (in parentesi sono indicati gli induttivi posizionati nella capriata adiacente a quella sottoposta a prova).
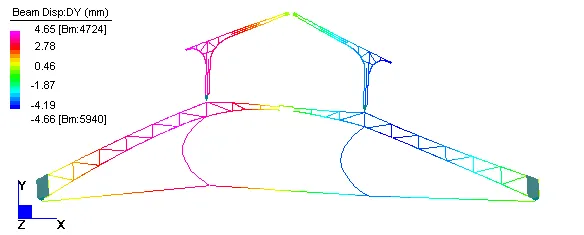
Figura 3. I° modo traslazionale in direzione trasversale, deformata modale della sola capriata trasversale intermedia (f =3,320Hz).
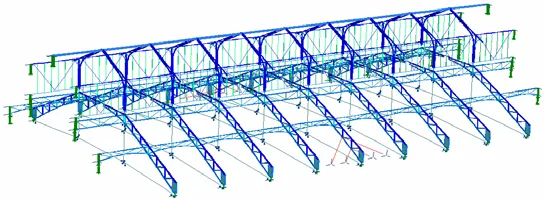
Figura 4. Modello di calcolo FEM spaziale.