Nell’ambito della progettazione di una copertura in acciaio e vetro di grande luce, si è reso necessario approfondire il comportamento dinamico dell’arco tipico, a travatura reticolare con catena inferiore, conducendo analisi dinamiche non lineari con il software di calcolo Straus7. L’analisi è stata condotta imponendo un’eccitazione ai vincoli di base tramite uno spostamento sinusoidale verticale con ampiezza di accelerazione costante e frequenza variabile, in modo crescente (analisi forward) o decrescente (analisi backward). In particolare, ogni frequenza della forzante viene mantenuta per un numero sufficiente di periodi da permettere di distinguere la risposta transitoria da quella stazionaria. Sono state così eseguite diverse simulazioni aumentando progressivamente l’accelerazione.
La risposta della struttura è stata sintetizzata in diagrammi di risposta in frequenza, riportando per ogni frequenza e accelerazione, il massimo spostamento del punto di controllo ottenuto dalla risposta dinamica stazionaria. Tali analisi hanno permesso di classificare il comportamento dinamico della struttura in funzione della frequenza e dell’ampiezza di eccitazione.
Per bassi livelli di eccitazione la risposta coincide con la risposta da analisi modale con catena attiva (fn). All’aumentare dell’ampiezza della forzante, si nota una riduzione della frequenza critica che amplifica la risposta (comportamento softening). Questo aspetto è sottolineato dai maggiori spostamenti ottenuti dalle analisi backward riportate in linea tratteggiata. La riduzione della frequenza critica si assesta al 60% della frequenza naturale per ampiezze elevate della forzante.
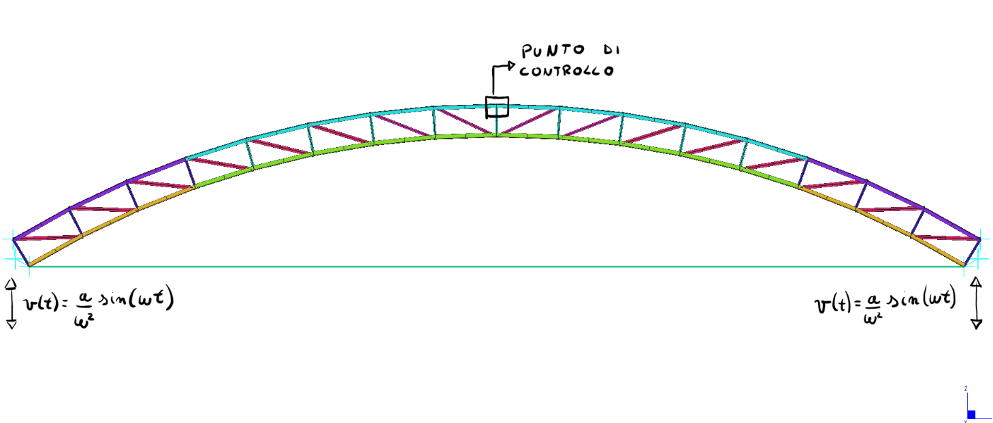
Figura 1: Modello FEM dell’arco e individuazione del punto di controllo e dei punti vincolati ai quali viene applicata la forzante esterna
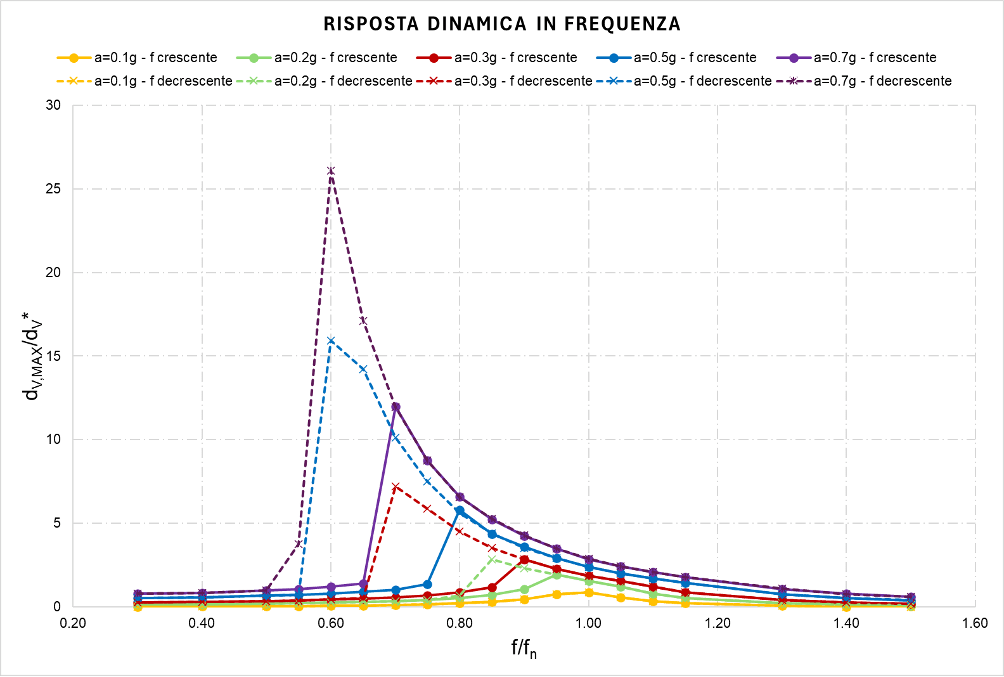
Figura 2: Risposta dinamica in frequenza dell’arco per diversi livelli di eccitazione
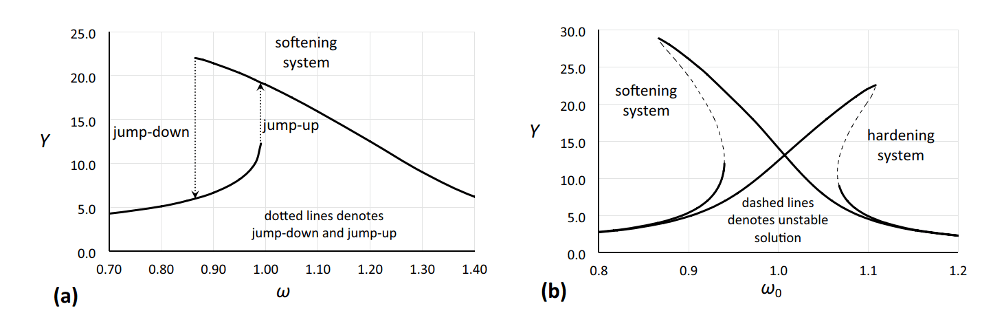
Figura 3: Si noti come la risposta dinamica in frequenza dell’arco rispecchi il comportamento atteso per sistemi di tipo softennig